Så var det dags att gnugga geniknölarna för sporthojsfolket. 
Har en liten uppgift jag skulle behöva hjälp med att lösa (se bifogad bild). Det jag har kommit fram till är:
V = Pi/3(r - v*r/360) * Sqrt(r^2-(r-v*r/360)^2)
där
V = konens volym
r = radien för cirkeln
v = cirkelsektorns vinkel
Sqrt = Roten ur
Tycker detta verkar vara en för omständig lösning, speciellt då jag kommer behöva derivera den med avseende på v för att finna max och minpunkterna. Så vad är det jag har missat? Går det att göra på något enklare sätt?
MvH
spiken
Har en liten uppgift jag skulle behöva hjälp med att lösa (se bifogad bild). Det jag har kommit fram till är:
V = Pi/3(r - v*r/360) * Sqrt(r^2-(r-v*r/360)^2)
där
V = konens volym
r = radien för cirkeln
v = cirkelsektorns vinkel
Sqrt = Roten ur
Tycker detta verkar vara en för omständig lösning, speciellt då jag kommer behöva derivera den med avseende på v för att finna max och minpunkterna. Så vad är det jag har missat? Går det att göra på något enklare sätt?
MvH
spiken


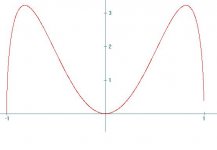
 fast det faller lite på latheten. Ska äta lunch nu, får se om jag orkar sen
fast det faller lite på latheten. Ska äta lunch nu, får se om jag orkar sen 









