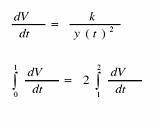Nexor
Full gas, mera ras?
Nu är jag lite kass men framför allt lat när det gäller matte och undrar däför om någon vänlig själv vill hjälpa mig med en uppgift? Här kommer problemtexten:
"Klockan åtta på julaftons morgon börjar tomtefar det mödosamma arbetet att skotta den smala
vägen genom skogen. Han skottar med en hastighet som är omvänt proportionell mot snödjupet i
kvadrat. Nissarna noterade att tomtefar skottade dubbelt så långt under den första timman som
under den andra. Eftersom de läst lite (ODE) på fritiden kunde de glatt överraska honom med att
ange den tidpunkt då det började snöa. Kan ni det också? Gör samma antagande som de morgontrötta
nissarna, nämligen att det snöade med jämn intensitet hela tiden."
Det är alltså differentialekvationer det handlar om, jag har försökt att ställa upp en med det blir fel. Jag använder mathematica för att slippa räkna för hand
Någon som orkar formulera fram nåt vettigt med begynnelsevärden osv? Snälla, jag bjuder på en piggelin som tack! 
"Klockan åtta på julaftons morgon börjar tomtefar det mödosamma arbetet att skotta den smala
vägen genom skogen. Han skottar med en hastighet som är omvänt proportionell mot snödjupet i
kvadrat. Nissarna noterade att tomtefar skottade dubbelt så långt under den första timman som
under den andra. Eftersom de läst lite (ODE) på fritiden kunde de glatt överraska honom med att
ange den tidpunkt då det började snöa. Kan ni det också? Gör samma antagande som de morgontrötta
nissarna, nämligen att det snöade med jämn intensitet hela tiden."
Det är alltså differentialekvationer det handlar om, jag har försökt att ställa upp en med det blir fel. Jag använder mathematica för att slippa räkna för hand
Någon som orkar formulera fram nåt vettigt med begynnelsevärden osv? Snälla, jag bjuder på en piggelin som tack! 
