MR.duDe
hejhej
Övar inför kursprov snart, och har två små problem jag behöver lösa utan miniräknare.
Den första uppgiften:
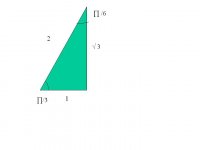
Beräkna f´(pi /3) då f(x)=2sin(x)
Om man deriverar f(x) får man ju 2cos(x). Alltså är 2cos(pi/3)=(pi/3).
Men pi/3 borde ju bli ungefär 1. Och då får man ju cos(1), och det är ju också ungefär 1. Då har man alltså kvar 2*1 vilket är 2. Men svaret ska vara 1.
Någon som vet vart jag gjort fel?
Det andra är:
Bestäm g(x) om g´(x)=sin(3x)+cos(2x) och g(pi)=2
Jag är med så långt som att man ska ha en primitiv funktion till g´, men när jag gör den kommer jag bara hit:
g(x)= -(cos(3x)/3)+(sin(2x)/2)
Men enligt svaren ska man även ha "+(5/3)" med på slutet. Vart kom det ifrån? och var har "g(pi)" med det hela att göra?
Den första uppgiften:
Beräkna f´(pi /3) då f(x)=2sin(x)
Om man deriverar f(x) får man ju 2cos(x). Alltså är 2cos(pi/3)=(pi/3).
Men pi/3 borde ju bli ungefär 1. Och då får man ju cos(1), och det är ju också ungefär 1. Då har man alltså kvar 2*1 vilket är 2. Men svaret ska vara 1.

Någon som vet vart jag gjort fel?
Det andra är:
Bestäm g(x) om g´(x)=sin(3x)+cos(2x) och g(pi)=2
Jag är med så långt som att man ska ha en primitiv funktion till g´, men när jag gör den kommer jag bara hit:
g(x)= -(cos(3x)/3)+(sin(2x)/2)
Men enligt svaren ska man även ha "+(5/3)" med på slutet. Vart kom det ifrån? och var har "g(pi)" med det hela att göra?

 Är med på uppgift 2 nu, men fattar fortfarande inte hur det kan bli 1 på första uppgiften, för om jag slår in 2cos(pi/3) på miniräknaren får jag också ut 1.9xxxx
Är med på uppgift 2 nu, men fattar fortfarande inte hur det kan bli 1 på första uppgiften, för om jag slår in 2cos(pi/3) på miniräknaren får jag också ut 1.9xxxx